在微积分学中，导数是一个核心概念，它描述函数值随自变量变化的速率，一阶导数描述函数在某点的斜率，二阶导数则描述斜率的变化率，以此类推，n阶导数则涉及到更高阶的变化情况，本文将深入探讨n阶导数的概念、性质、计算方法和应用。

n阶导数的概念与性质

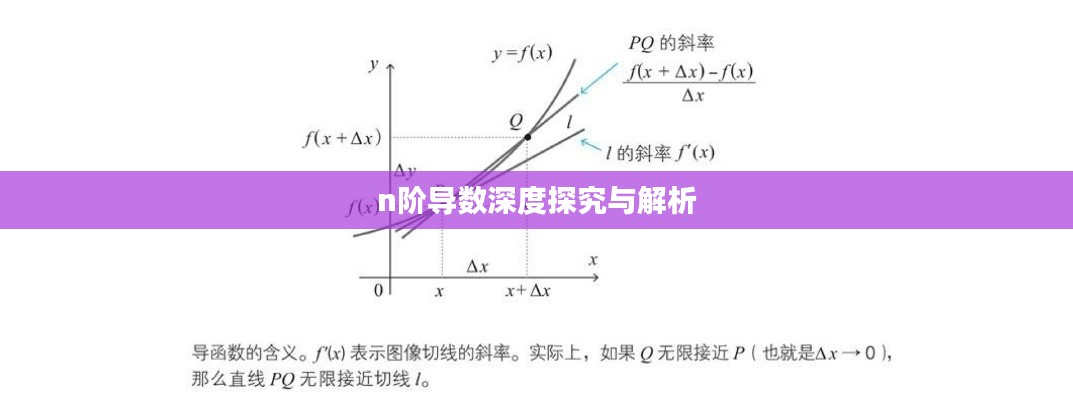
n阶导数，即函数关于自变量的高阶导数，对于函数f(x)，其一阶导数为f'(x)，二阶导数为f''(x)，以此类推，n阶导数表示为f(n)(x)，在理解n阶导数的概念后，我们需要掌握其一些基本性质，常数函数的任何阶导数都为0，基本初等函数的n阶导数公式等，这些性质和公式是计算n阶导数的基础。

n阶导数的计算方法

计算n阶导数，除了基本的导数计算规则外，还需要掌握一些特殊的方法，利用莱布尼茨公式计算高阶导数，这种方法对于多项式函数特别有效，对于复杂函数，可能需要使用到微分法则的反复应用，如链式法则、乘积法则和商数法则等，在实际计算中，还需要注意一些计算技巧，如合并同类项、化简表达式等。

n阶导数的应用

n阶导数在物理、工程、经济等领域有广泛的应用，在物理中，n阶导数可以描述物体的运动状态及其变化率；在工程领域，可以用来描述系统的动态行为；在经济领域，可以用来分析经济模型的动态变化等，n阶导数在数学理论研究中也有重要作用，如研究函数的性质、求解方程等。

专题研究：n阶导数与函数性质的关系

研究n阶导数与函数性质的关系是深入理解导数的关键，通过探讨不同类型的函数（如多项式函数、三角函数、指数函数等）的n阶导数，我们可以揭示函数的一些重要性质，通过计算函数的泰勒级数展开式，我们可以利用n阶导数来分析函数的局部和全局行为，通过研究函数的单调性、极值点等性质与n阶导数的联系，我们可以更深入地理解函数的性质和行为。

本文深入探讨了n阶导数的概念、性质、计算方法和应用，通过专题研究，我们进一步揭示了n阶导数与函数性质的关系，在实际应用中，我们需要根据具体问题选择合适的导数计算方法，并深入理解导数与函数性质的联系，未来研究方向包括进一步研究n阶导数在各个领域的应用，以及探索更高效的计算方法。

参考文献

（此处列出相关的参考文献）

通过本文的学习，读者可以全面了解n阶导数的相关知识，为进一步学习和应用微积分打下坚实的基础。